男朋友问哪里想我了怎么回复 我男朋友在哪里
一、男朋友问哪里想我了怎么回复如果一个男人说想你了的情况,那么一定要注意把握分寸,要注意看你跟这个男人之间是什么样的一个关系,如果是比较亲密的情侣关系,或者是彼此之间有那么一些暗恋的情愫,那么可以用比较温柔的话语进行回答,如果两个人仅仅是普
一、男朋友问哪里想我了怎么回复
如果一个男人说想你了的情况,那么一定要注意把握分寸,要注意看你跟这个男人之间是什么样的一个关系,如果是比较亲密的情侣关系,或者是彼此之间有那么一些暗恋的情愫,那么可以用比较温柔的话语进行回答,如果两个人仅仅是普通的朋友或者是处于某一方单相思的情况下,最好还是不要乱回答,仅仅就按照正常朋友的回答就可以了。
二、为什么我男朋友给我报告他的行踪,在干啥干啥
男朋友向你主动报备他的行踪,都在干什么,或者是干了点儿什么,是对你的一种在乎和尊重。是想让你对他放心,对他有信心。面对这种情况,你应该积极回应他的热情报告,能够提出建议的时候,提点儿建议。还要不忘让他注意身体,别太累了,让他知道你也在乎他。
三、男朋友问去哪里玩怎么回答
男朋友问去哪里玩,你可以说,我不知道哪里好玩,你可以推荐几个地方看看,然后决定去哪里玩可以吗。我觉得你可以实话实说,因为他是你的男朋友。例如,你们异地恋,你去他那里找他玩,他说去哪里玩,那你肯定不知道啊,但是你让他介绍几个地方来玩,你就知道选择去哪里了,最主要的事和你在一起去哪里玩都行
四、男朋友问你今晚去哪里了怎么回答
可以回答说我今晚去了闺蜜那里,和她一起度过了一个美好的生日,请不要对我有所猜疑,整天的对我进行怀疑会让我内心对你产生厌恶,希望你一定要尊敬我,不要对我的私生活造成打扰,否则严重的后果你将承担不起。只有这样带着严肃的态度去回答男友让她明白做人的原则,平时多做点交流才能避免误会的发生。
相关文章
-
男篮亚洲杯决赛赛程 亚洲杯男篮决赛详细阅读

1、7月12日 2、12:00 中国台北-巴林3、16:00 约旦-澳大利亚4、18:30 沙特-印尼5、21:00 中国-韩国6、7月13日 7、12:00 印度-新西
-
最炫民族风谁唱的 王广场舞最炫民族风详细阅读

1、原唱凤凰传奇2、最炫民族风3、作词 : 张超4、作曲 : 张超5、苍茫的天涯是我的爱6、绵绵的青山脚下花正开7、什么样的节奏是最呀最摇摆8、什么样的歌声才是最开怀9、弯弯的河水从天上来10、流向那万紫千红一片海11、火辣辣的歌谣是我们的
-
成都到广东阳江市阳西县海陵岛自驾怎么走 阳江海陵岛攻略详细阅读

驾车路线:全程约1681.6公里 起点:成都市1.成都市内驾车方案1) 从起点向正西方向出发,沿人民东路辅路行驶60米,左转进入人民中路一段2) 沿人民中路一段行驶40米,过右侧的成都博物馆新馆,稍向左转进入人民中路3) 沿人民中路行驶50
-
佐菲奥特曼数据设定 佐菲奥特曼全集详细阅读

佐菲·奥特曼是圆谷特摄剧《奥特曼》系列的登场角色,是奥特兄弟中的大哥,也是宇宙警备队的队长,地位上仅次于奥特之父。佐菲有着出色的领导能力以及强大的实力,更拥有奥特兄弟技能中单体威力最大的M87光线作为必杀技,使其深受众人信赖。佐菲平日坐镇于
-
摩比爱数学大班飞跃篇怎么教 大班数学公开课详细阅读

《摩比爱数学大班飞跃篇》是一套针对小学生的数学教材,主要旨在培养学生的数学思维能力和解决问题的能力。以下是教授《摩比爱数学大班飞跃篇》的一般方法: 1. 熟悉教材:教师需要仔细研读教材,了解每个章节的教学目标、教学内容和教学方法。2. 设计
-
最好的纯牛奶是什么牌 目前中国最好的牛奶详细阅读

1、纯牛奶十大品牌排行榜。2、第一名:伊利3、4、伊利不仅是健康食品的提供者,同时也是健康生活方式的倡导者。伊利纯牛奶全程有机,保留每一滴牛奶的自然纯粹。纯脱脂,零添加,助力好身材,保持轻盈,轻松获得好曲线,开启健康好生活。5、第二名:蒙牛
-
现金流量表附表的存货怎么计算 现金流量表公式详细阅读
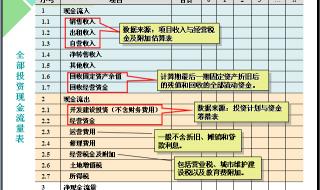
在编制现金流量表附表时,一般来说,存货的增减变动应该与资产负债表中的存货增减变动是一致的。但也存在一些特殊因素,在编制附表时应予以考虑并调整,否则会导致主附表的经营活动现金流量不平衡。主要因素为:1.存货计提了跌价准备。存货跌价准备的增减变
-
潘玮柏几岁啦 潘玮柏主演的电视剧详细阅读

1、42周岁 2、潘玮柏(Wilber Pan),1980年8月6日出生于美国西弗吉尼亚州,祖籍中国上海市普陀区,华语流行乐男歌手、影视演员、主持人,毕业于加州州立理工大学。2001年3月,担任Channel[V]音乐台的主持人,从而正式进
-
使用whatsapp软件发送图片,接收很模糊,了解的是这个软件把图片压缩了,软件对图片的要求或者怎么解决 图片放大不失真软件详细阅读

1、通过邮箱发送的话就不会进行压缩图片。2、很多软件都会进行压缩,然后以达到传输的更快。3、通过邮箱发送的话就不会进行压缩图片。4、很多软件都会进行压缩,然后以达到传输的更快。5、通过邮箱发送的话就不会进行压缩图片。6、很多软件都会进行压缩
-
polo如何改装17寸轮毂 新polo改装详细阅读

改装汽车轮毂需要考虑一些因素,包括车辆的具体型号、品牌、轮毂规格和个人喜好。以下是大致的步骤:1. 确定尺寸:首先,确保购买的17寸轮毂适用于您的车辆。查询车辆的规格和制造商建议的合适轮毂尺寸,以确保匹配。2. 选择样式:浏览不同的轮毂样式
-
小学生7人上课时的搞笑小品剧本 小学生小品剧本详细阅读

一天, 老师走进课堂,学生们一齐起立喊:“老师早上好!” 老师愤愤地说:“只叫早上好?那我下午呢?难道就不好了吗?” 于是学生们又一齐喊:“老师下午好!” 老师说道:“坐下!今天我们要复习反义词,我们这样练习,我说一句,你们大声说出反
